Mathe

Bruchrechnung
Brüche sind bei Schülern nicht sehr beliebt. Vielleicht weil sie einfach so anders sind als "normale" Zahlen. Im Matheunterricht hat man bestimmte Regeln gelernt (und endlich verstanden), doch bei Brüchen sind diese nun scheinbar nicht mehr gültig.
Die Bruchzahlen sind eben keine ganz "normale" Zahlen, sondern beschreiben einen Zahlenraum zwischen zwei ganzen Zahlen.
Das kann man sich ein bisschen wie die Millimeterstriche auf einem Lineal vorstellen. Die Zentimeterstriche sind die ganzen Zahlen und dazwischen befinden sich die Bruchzahlen. Nur gibt es viel mehr Bruchzahlen zwischen den ganzen Zahlen, als auf dem Lineal.

Bruchzahlen beschreiben aber auch einen Rechenvorgang. Sie zeigen nämlich wie oft ein Ganzes zerteilt wurde.
Zuerst lernt man ja, dass man kleine Zahlen nicht durch große teilen lassen. Brüche machen das aber möglich:
1:3=? Diese Rechnung lässt sich als Bruchzahl schreiben:
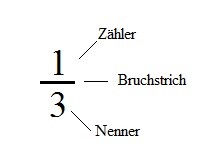
Das kann man sich z.B. auch mit einer Pizza, Torte, Schokoladentafel oder sonst etwas leckerem vorstellen. Die Pizza steht dabei für die Zahl 1. Sie soll in sechs gleichgroße Teile eingeteilt werden. Zack! Jetzt hat man eine Pizza die aus sechs gleichgroßen Teilen besteht. Mathematisch hat man nichts anderes gemacht, als 1:6 zu rechnen.

Rechenregeln
Wichtig ist, dass man sich hier nicht verrückt machen lassen darf. Jeder kann Bruchrechnen und du auch!
Und hier kommt auch schon der Beweis:
1 + 1 = 2
1cm + 1cm = 2cm
1kg + 1kg = 2kg
1Apfel + 1Apfe l= 2Äpfel
1/3 + 1/3 = 2/3
Es gibt aber natürlich etwas mehr zu beachten:
Brüche
Informiert euch mit Hilfe dieser drei Videos über Kürzen, Erweitern, Addieren, Subtrahieren und Dividieren von Brüchen! Hast du alles verstanden?
Mit Hilfe dieser Arbeitsblätter könnt ihr das Rechnen mit Brüchen trainieren.
